Atención : Busco Autores y Editores para colaborar con Mi blog.

Pasos A seguir

1- Debes seguir mi Usuario De google

2-Comentar la entrada con tu Correo Electronico

3-me comunicaría contigo y Te pediría Preparar un material de tu autoria , Nada Copiado de Internet directamente , pero si debes apoyarte en algún material. 

4-El post se somete a revisión si pasas la prueba , te Acreditó como Editor de blog. 

Introducciòn a los Oxidos Bàsicos

ÓXIDOS BÁSICOS

      

El el tipo de Compuesto Químico que se Forma por la Unión Ionica de algún metal (electropositivo) y el oxigeno (electronegativo). 

¿QUIENES SON METALES?

La mayor parte de los elementos metálicos exhibe el lustre brillante que asociamos a los metales. Los metales conducen el calor y la electricidad, son maleables (se pueden golpear para formar láminas delgadas) y dúctiles (se pueden estirar para formar alambres). Todos son sólidos a temperatura ambiente con excepción del mercurio (punto de fusión =-39 ºC), que es un líquido. Dos metales se funden ligeramente arriba de la temperatura ambiente: el cesio a 28.4 ºC y el galio a 29.8 ºC. En el otro extremo, muchos metales se funden a temperaturas muy altas. Por ejemplo, el cromo se funde a 1900 ºC.

Los metales tienden a tener energías de ionización bajas y por tanto se oxidan (pierden electrones) cuando sufren reacciones químicas.

LOCALIZACIÓN EN LA TABLA PERIÓDICA

Corresponde a los elementos situados a la izquierda y centro de la Tabla Periódica (Grupos 1 (excepto hidrógeno) al 12, y en los siguientes se sigue una línea quebrada que, aproximadamente, pasa por encima de Aluminio (Grupo 13), Germanio (Grupo 14), Antimonio (Grupo 15) y Polonio (Grupo 16) de forma que al descender aumenta en estos grupos el carácter metálico).

EL OXIGENO 

Elemento químico gaseoso, símbolo O, número atómico 8 y peso atómico 15.9994. Es de gran interés por ser el elemento esencial en los procesos de respiración de la mayor parte de las células vivas y en los procesos de combustión. Es el elemento más abundante en la corteza terrestre. Cerca de una quinta parte (en volumen) del aire es oxígeno.

Existen equipos capaces de concentrar el oxígeno del aire. Son los llamados generadores o concentradores de oxígeno, que son los utilizados en los bares de oxígeno.

El oxígeno gaseoso no combinado suele existir en forma de moléculas diatómicas, O2, pero también existe en forma triatómica, O3, llamada ozono.

El oxígeno se separa del aire por licuefacción y destilación fraccionada. Las principales aplicaciones del oxígeno en orden de importancia son: 1) fundición, refinación y fabricación de acero y otros metales; 2) manufactura de productos químicos por oxidación controlada; 3) propulsión de cohetes; 4) apoyo a la vida biológica y medicina, y 5) minería, producción y fabricación de productos de piedra y vidrio.

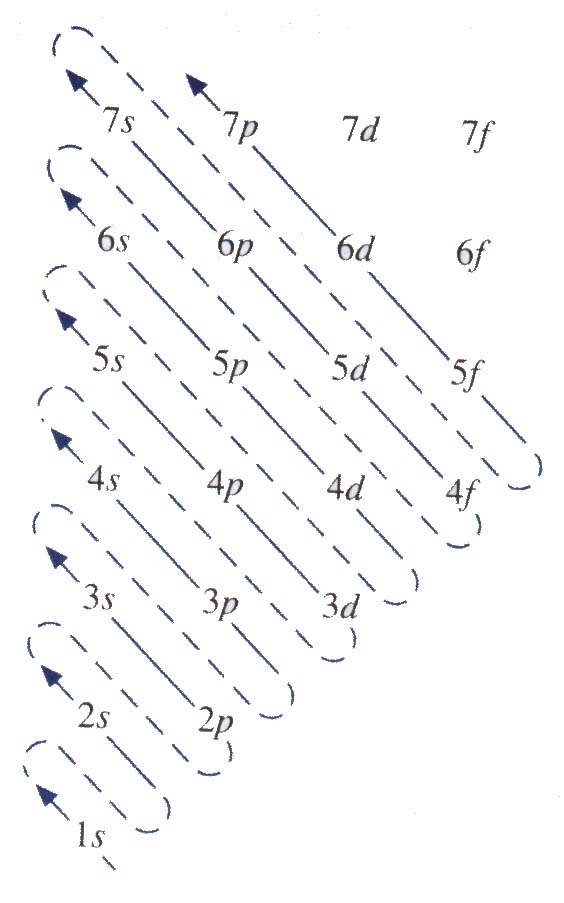
CONFIGURACIÓN ELECTRONICA

CONFIGURACIÓN ELECTRÓNICA DE METALES DE TRANSICIÓN 

Los elementos del escandio (Z=21) al cobre (Z=29) pertenecen a los metales de transición. Los metales de transición tiene el subnivel d incompleto, o bien dan lugar a cationes que tienen el subnivel d incompleto. Considérese los metales de la primera serie de transición, del escandio al cobre. A lo largo de esta serie los electrones que se agregan se colocan en los orbitales 3d de acuerdo con la regla de Hund. Sin embargo hay dos irregularidades.

La configuración del cromo (Z=24) es [Ar] 4s13d5 y no [Ar] 4s23d4, como se esperaría. Se observa peculiar similitud en el cobre, cuya configuración electrónica es [Ar] 4s13d10 en lugar de [Ar] 4s23d9. Lo que ocurre es que la energía de los orbitales 3d y 4s se encuentran muy relacionadas entre sí. De manera ocasional, un electrón puede moverse desde uno de estos orbitales hasta el otro orbital. Este comportamiento anómalo se debe en particular a la estabilidad especial que se asocia a los orbitales degenerados que se encuentran llenos de manera incompleta.

Para los elementos del Zn (Z=30) al Kr (Z=36), las subcapas 4s y 4p se llenan en la forma indicada. En el rubidio (Z=37), los electrones empiezan a entrar en el nivel energético n=5 iniciando la quinta fila de la tabla periódica la cual es muy similar a la que precede. La sexta fila empieza muy parecida a la quinta fila: Un electrón en el orbital 6s del cesio (Cs) y dos electrones en el orbital 6s del bario (Ba). El siguiente elemento el latano (La) es un metal de transición. 

Según el diagrama de llenado de los orbitales, después de llenar el orbital 5s se colocaran los electrones en el orbital 4f . En realidad las energías del 5d y el 4f están muy cerca, de hecho para el latano el 4f es ligeramente de mayor energía que el 5d. La configuración del latano es [Xe] 6s25d1y no [Xe] 6s24f1. Siguiendo al latano están los catorce elementos que conforman las tierras raras o lantánidos. Los metales de las tierras raras tiene incompletos los subniveles 4f o fácilmente dan lugar a cationes que tienen subniveles 4f incompletos. En esta serie, los electrones que se agregan se colocan en los subniveles 4f. Después de que se han llenado por completo el siguiente electrón entra en el subnivel 5d, lo que ocurre en el lutecio.

Nótese que la configuración electrónica del gadolinio (Z=64) es [Xe] 6s24f75d1 en lugar de [Xe] 6s24f8. De nueva se gana mayor estabilidad al tener subniveles semilleros (4f7) y ello favorece a esta configuración como en el caso del cromo.

Una vez completada la serie de los lantánido, siguen los metales de la tercera serie de transición incluyendo lantano y hafnio (Z=72) hasta oro (Z=79), que se caracterizan por el llenado de los orbitales 5d. A continuación se llenan los orbitales 6p que siguen hasta radón (Z=86).

La última fila de los elementos pertenece a la serie de los actínidos, la cual comienza con torio (Z=90). La mayoría de estos elementos no se encuentran en la naturaleza, sino que han sido sintetizados en reacciones nucleares.

Para nombrarlos se utilizan tres sistemas de nomenclaturas muy conocidas:

A) Sistemática: se utilizan los siguientes prefijos para indicar la cantidad de átomos de cada elemento que componen al óxido:

Mono = Si está una sola vez. 

Di = si se repite dos veces

Tri = Tres veces

Tetra = Cuatro veces

Penta = Cinco veces

Hexa = Seis veces

Hepta = Siete veces

Por ejemplo: Fe2O3 : Trióxido de dihierro

                     CuO: Monóxido de cobre.  

(se sobreentiende que al no colocar mono como prefijo, el elemento está una sola vez en la fórmula)

                      

B) Stock: En esta nomenclatura se debe colocar el número de oxidación del elemento electropositivo (metal) en número romano dentro de un paréntesis.

Por ejemplo: Fe2O3 : Óxido de hierro (III)

                     CuO: Óxido de cobre (II)

C) Tradicional: En esta nomenclatura se utilizan prefijos y sufijos dependiendo del número de estados de oxidación que presente el elemento electropositivo (metal).

a) Si el elemento electropositivo presenta un sólo estado de oxidación: se coloca la palabra "Óxido de" seguido del nombre del elemento electropositivo en español. Por ejemplo: 

CaO: Óxido de calcio. 

 Al2O3: Óxido de aluminio.

b) Si el elemento electropositivo presenta dos números de oxidación: Se coloca la palabra "Óxido" seguido de las terminaciones "oso" o "ico" al elemento electropositivo respectivamente (generalmente se utiliza el nombre en Latin del elemento menos la terminación "um o ium"). Por ejemplo:  FeO : Óxido Ferroso.

                                                               Fe2O3 : Óxido Férrico.

c) Si el elemento electropositivo presenta tres números de oxidación: Se coloca "Óxido" seguido de:

c.1) Hipo+ nombre del metal en Latin menos su terminación "um o ium"+oso.   Si es el menor número de oxidación.

c.2) Nombre del metal en Latin menos su terminación "um o ium"+oso.  Si es el penúltimo número de oxidación.

c.3) Nombre del metal en Latin menos su terminación "um o ium"+ico. Si es el último número de oxidación.

Por ejemplo:   CrO: Oxido hipocromoso.

                       Cr2O3 : Óxido cromoso.

                       CrO3 : Óxido crómico.  

EJERICICIOS PROPUESTOS.

1- NOMBRE MEDIENTE LAS 3 NOMENCLATURAS LOS SIGUIENTES OXIDOS BÀSICOS:

1- FeO 
2- MgO 
3- CuO 
4- MnO 
5- CaO 
6- K2O (el numero corresponde al subíndice) 
7- ZnO 
8- Na2O 
9- Ag2O 
10- Rb4O2 
11- Sr2O2 

EJERCICIO DE GAS IDEAL EXPLICACIÓN RÁPIDA

Problemas.

1) En la figura 2 kg de argón y 2 kg de N₂ se encuentran ocupando igual volúmenes de 0.5 m³ cada uno y separados por un pistón sin fricción y no conductor del calor; la temperatura del argón es de 50 °C. Se le suministra calor a ambos recipientes hasta conseguir un incremento de temperatura en el argón de 200 °C. Determínese las temperaturas iniciales y finales del N_2.

    

Como  P_A1 = P_B1  tenemos:

   

Suponiendo volúmenes iguales:

Simplificando tenemos:

2) Un tanque de 1 m³ que contiene aire a 25 °C y 500 kPa se conecta por medio de una válvula, a otro tanque que contiene 5 kg de aire a 35 °C Y 200 kPa. Después se abre la válvula y se deja que todo el sistema alcance el equilibrio térmico con el medio ambiente que se encuentra a 20 °C. Determine el volumen del segundo tanque y la presión final del aire.

Tanque A                           Tanque B

 

Tanque B

Tanque A

Volumen final del sistema

Masa final del sistema

Presión final del sistema

Gases ideales Teoría

GASES IDEALES

        La necesidad de estudiar los gases ideales se explica porque los gases son fluidos ampliamente utilizados en una gran variedad de sistemas como son los compresores y las turbinas a gas.

LEY DE BOYLE

        Hacia el año 1660, Robert Boyle realizó una serie de experiencias, con las que determinó el efecto que ejerce la presión sobre el volumen de una determinada cantidad de aire.

Fig. 1.25 Representación de la Ley de Boyle

“El volumen de un gas varía de forma inversamente proporcional a la presión si la temperatura permanece constante.”

LEY DE CHARLES Y GAY LUSSAC

      En 1787 Charles y posteriormente Gay Lussac en 1808 demostraron que, si la presión permanece constante el volumen del gas varía en forma lineal con la temperatura.

Fig. 1.26 Representación de la Ley de Charles

Para        t = 0ºC         V = V₀        

y para   t = -273.15ºC        V = 0

                  

       La extrapolación a bajas temperaturas de dichas rectas es muy significativa pues tiende a V = 0 cuando la temperatura tiende a  -273.15ºC lo que aconseja la elección de una escala cuyo origen sea precisamente esta temperatura. Esta escala es la ya conocida escala Kelvin:

 

Este resultado expresa la ley de Charles-Gay Lussac que puede enunciarse así:

“El volumen de una determinada cantidad de gas varía en proporción directa con la temperatura si la presión permanece constante.”

      Estas leyes la cumplen aproximadamente la mayor parte de los gases, constituyendo ambas leyes dos características de los gases que se denominan ideales.

LEY DE LOS GASES IDEALES

       Las leyes de Boyle y de Charles pueden cambiarse para proporcionarnos una ley más general que relacione la presión, el volumen, y la temperatura.

    Consideremos una masa de gas que ocupa un Volumen V₁ a la temperatura T₁ y presión P₁. Supongamos que manteniendo constante la temperatura T₁, se produce una interacción mecánica entre el sistema y el medio exterior, de forma que la presión alcanza el valor P₂ y el volumen que ocupa el gas se convierte en V_x. Para este proceso se cumplirá según la ley de Boyle

                                                 

Si a continuación el gas interacciona térmicamente con el medio exterior, su presión seguirá siendo P₂ mientras que la temperatura pasará a T₂ y por consiguiente el volumen alcanzará el valor V₂. Para este proceso de acuerdo con la ley de Charles

            

Igualando las ecuaciones 1.40 y 1.41 se obtiene:

                                                                                        

      El valor de la constante se determina a partir de las consideraciones de Avogadro. Este hace uso de razonamientos de naturaleza microscópica para justificar el comportamiento macroscópico de la materia de diferentes gases, que a la misma presión y temperatura contienen el mismo número de moléculas; deduce que en un mol de cualquier sustancia existe el mismo número de moléculas que calcula en 6.023x10²³ .

Para un mol la hipótesis de Avogadro se suele formular diciendo que los volúmenes ocupados por un mol de cualquier gas a igual presión y temperatura son iguales.

      Experimentalmente se comprueba que a 1 atm de presión y a una temperatura de 0ºC ese volumen es 22. 4136 l  (SI 101.325 kPa ; 0ºC, 1 kmol ocupará un volumen de 22.4136 m³ ).

      El resultado dado por la ecuación puede expresarse en función del número de moles de la sustancia, ya que el volumen es proporcional a dicho número; luego podrá escribirse:

                

donde n = m / M   siendo m la masa en kg y M la masa molecular del gas

                            

sustituyendo en 1.44 la constante universal

Otras formas:

                                                                   

Donde R es la constante específica para cada gas.

EJERICICIOS DE GASES IDEALES

1.- Una cantidad de gas ocupa un volumen de 80 cm³ a una presión de 750 mm Hg. ¿Qué volumen ocupará a una presión de 1,2 atm.si la temperatura no cambia?

Como la temperatura y la masa permanecen constantes en el proceso, podemos aplicar la ley de Boyle: P₁.V₁ = P₂.V₂

 Tenemos que decidir qué unidad de presión vamos a utilizar. Por ejemplo atmósferas.

Como 1 atm = 760 mm Hg, sustituyendo en la ecuación de Boyle:

2.- El volumen inicial de una cierta cantidad de gas es de 200 cm³ a la temperatura de 20ºC. Calcula el volumen a 90ºC si la presión permanece constante.

Como la presión y la masa permanecen constantes en el proceso, podemos aplicar la ley de Charles y Gay-Lussac:

V1/T1=V2/T2

El volumen lo podemos expresar en cm³ y, el que calculemos, vendrá expresado igualmente en cm³, pero la temperatura tiene que expresarse en Kelvin.

3.- Una cierta cantidad de gas se encuentra a la presión de 790 mm Hg cuando la temperatura es de 25ºC. Calcula la presión que alcanzará si la temperatura sube hasta los 200ºC.

Como el volumen y la masa  permanecen constantes en el proceso, podemos aplicar la ley de   Gay-Lussac:

P1/T1=P2/T2

La presión la podemos expresar en mm Hg y, la que calculemos, vendrá expresada igualmente en mm Hg, pero la temperatura tiene que expresarse en Kelvin.

4.- Disponemos de un recipiente de volumen variable. Inicialmente presenta un volumen de 500 cm³ y contiene 34 g de amoníaco. Si manteniendo constante la P y la T, se introducen 68 g de amoníaco, ¿qué volumen presentará finalmente el recipiente?

Ar (N)=14. Ar (H)=1.

Manteniendo constante la P y la T, el volumen es directamente proporcional al número de moles del gas. El mol de amoníaco, NH₃, son 17 g luego:

 Inicialmente  hay en el recipiente 34 g de gas que serán 2 moles y al final hay 192 g de amoníaco que serán 6 moles.

EJERCICIOS PROPUESTOS 

5.- Un gas ocupa un volumen de 2 l en condiciones normales. ¿Qué volumen ocupará esa misma masa de gas a 2 atm y 50ºC? R: 1,18lt

6.- Un recipiente cerrado de 2 l. contiene oxígeno a 200ºC y 2 atm. Calcula:

a)  Los gramos de oxígeno contenidos en el recipiente.

b) Las moléculas de oxígeno presentes en el recipiente.

Ar(O)=16.

 R: a) 3,2 gr b) 6,023.10²²  MOLECULAS DE O₂

7.- Tenemos 4,88 g de un gas cuya naturaleza es SO2 o SO3. Para resolver la duda, los introducimos en un recipiente de 1 l y observamos que la presión que ejercen a 27ºC es de 1,5 atm. ¿De qué gas se trata?

Ar(S)=32.Ar(O)=16.

R: El gas es el SO₃

8.-Un mol de gas ocupa 25 l y su densidad es 1,25 g/l, a una temperatura y presión determinadas. Calcula la densidad del gas en condiciones normales.

 R. 1,40 gr/L

La Presión y sus unidades Químicas

PRESIÓN: Una medida del peso de la atmósfera que presiona sobre nosotros.

UNIDADES DE PRESIÓN 

Presión = Fuerza/Área = N/m

FACTORES PARA CONVERTIR UNIDADES DE PRESIÓN 

1 pascal (Pa) = 1 N/m2 

1 atm = 760 mmHg = 760 torr 

1 atm = 101,325 Pa 

Presión Atmosférica

Llamada “presión atmosférica,” o la fuerza ejercida sobre nosotros por la atmósfera que se encuentra encima.

Medida usando un barómetro – Un dispositivo que puede medir el peso de la atmósfera sobre nosotros

Presión manometrica.

Es la diferencia entre la presión absoluta o real y la presión atmosférica. Se aplica tan sólo en aquellos casos en los que la presión es superior a la presión atmosférica, pues cuando está cantidad es negativa se llama presión de vacío.

EN NUESTRO SIGUIENTE POST ESTAREMOS RESOLVIENDO EJERICIOS PARA CALCULAR LA PRESIÓN. 

Las Unidades de temperatura

La temperatura es una magnitud física que expresa el grado o nivel de calor o frío de los cuerpos o del ambiente. En el sistema internacional de unidades, la unidad de temperatura es el Kelvin. A continuación, de forma generalizada, hablaremos de otras unidades de medida para la temperatura.
En primer lugar podemos distinguir, por decirlo así, dos categorías en las unidades de medida para la temperatura: absolutas y relativas.

- Absolutas son las que parten del cero absoluto, que es la temperatura teórica más baja posible, y corresponde al punto en el que las moléculas y los átomos de un sistema tienen la mínima energía térmica posible.
         - Kelvin (sistema internacional): se representa por la letra K y no lleva ningún símbolo "º" de grado. Fue creada por William Thomson, sobre la base de grados Celsius, estableciendo así el punto cero en el cero absoluto (-273,15 ºC) y conservando la misma dimensión para los grados. Esta fue establecida en el sistema internacional de unidades en 1954.

- Relativas por que se comparan con un proceso fisicoquímico establecido que siempre se produce a la misma temperatura.
       - Grados Celsius (sistema internacional): o también denominado grado centígrado, se representa con el símbolo ºC. Esta unidad de medida se define escogiendo el punto de congelación del agua a 0º y el punto de ebullición del agua a 100º , ambas medidas a una atmósfera de presión, y dividiendo la escala en 100 partes iguales en las que cada una corresponde a 1 grado. Esta escala la propuso Anders Celsius en 1742, un físico y astrónomo sueco.
       - Grados Fahrenheit (sistema internacional): este toma las divisiones entre los puntos de congelación y evaporación de disoluciones de cloruro amónico. Así que la propuesta de Gabriel Fahrenheit en 1724, establece el cero y el cien en las temperaturas de congelación y evaporación del cloruro amónico en agua. Este utilizo un termómetro de mercurio en el que introduce una mezcla de hielo triturado con cloruro amónico a partes iguales. Esta disolución salina concentrada daba la temperatura más baja posible en el laboratorio, por aquella época. A continuación realizaba otra mezcla de hielo triturado y agua pura, que determina el punto 30 ºF, que después fija en 32 ºF (punto de fusión del hielo) y posteriormente expone el termometro al vapor de agua hirviendo y obtiene el punto 212 ºF (punto de ebullición del agua). La diferencia entre los dos puntos es de 180 ºF, que dividida en 180 partes iguales determina el grado Fahrenheit

FUENTE : http://www.pce-iberica.es/medidor-detalles-tecnicos/unidades-temperatura.htm

LA DENSIDAD, LA MASA Y EL VOLUMEN .

La densidad de una sustancia se define como la cantidad de masa que posee por unidad de volumen.

Densidad = masa (m) /Volumen (v)

La densidad es una propiedad intensiva y no depende de la cantidad de masa presente, para un material dado la relación de masa a volumen siempre es la misma; es decir, el volumen aumenta conforme aumenta la masa. Usualmente la densidad se expresa en g/mL, g/L, g/cc.

 EJEMPLOS 1. 

Densidad de una sustancia a partir de su masa y volumen: calcular la densidad del oro sabiendo que 50 g de esta sustancia ocupan 2.59 mL de volumen 

SOLUCIÓN

D = masa /V= 50 g/ 2.59mL = 19.33 g/mL 

EJEMPLO 2

Cálculo de la masa de un líquido contenido en un volumen dado: la densidad del etanol es 0.798 g/mL. Calcular la masa de 17.4 mL del líquido. 

SOLUCIÓN 

M = d x v=  0.798 g/mL x 17.4 mL = 13.9 g

EJEMPLO 3

Cálculo del volumen de una solución: la densidad de un alcohol es 0.8 g/cm . Calcular el volumen de 1600 g de alcohol

SOLUCIÓN

Primero se calcula el volumen del bloque Volumen = largo x ancho x altura 

V= 5.0 cm x 4.0 cm x 3.0 cm = 60 cm3

Luego despejando de la ecuación:

d = m/v = 474 g / 60 cm3 = 7.9 g/cm3  

EJERCICIOS PROPUESTOS

1. Calcule la densidad de un cuerpo cuya mas es 450000mg y cuyo volumen corresponde a estas dimensiones (250cmx450,55cmx17cm).

2.Determine la cantidad de volumen requerido para preparar 0,2467 kg de solucion a una densidad de 0,07183 kg/cc . Exprese todos los resultados en gr/ml.

3. Halle la masa de un cuerpo cuyas dimensiones son las siguientes (13mx14mx180m) y cuya densidad es igual a los 343,18 kg/cm³ . Exprese los resultados en gr/cm³ .

4. la densidad del agua es de 1gr/ml ¿Cuantos kg seran necesarios para preparar 2600 lt de solucion ?

5. La densidad del oro es de 19.3g/cm3 si se una utilizan 0,29 tonelas de oro¿ cuantos lt de solución de pueden preparar?

6. La densidad del plomo es de 11,4 g/ml si se tiene una solucion de 400cc ¿cual es la masa de plomo utilizada ?. exprese el resultado en mg. 

7.Calcule la densidad total de una solución cuyas fracciones de volumen son iguales a x1= 29,60  x2=12,40 x3=5,60 y cuya mas total es igual a 500gr.?

8.¿Determine cuantos litros de solución son necesarios para mezclar 1,24 toneladas de oro?

9. Se mezclan homogeneamente 2 masas : m1 = 40Kg m2 : 12kg en 120 ml de solución junto con volumen adicional de 2 lt . calcule:

a) el volumen total de la mezcla b)la masa total de la mezcla C) la densidad total de la mezcla en gr/ml d) la densidad en kg/ml.

El sistema internacional SI

Un sistema de unidades es un conjunto de unidades básicas o fundamentales que se toman como referencia; cada una de las unidades fundamentales representa una cantidad física determinada; las unidades que no aparecen entre las fundamentales se denominan unidades derivadas. Existen varios sistemas de unidades, cada uno de ellos tiene un determinado número de unidades básicas o fundamentales. 

Unidades fundamentales y derivadas En 1960 se llego a un acuerdo internacional que establecía un grupo dado de unidades métricas para emplearse en mediciones científicas. Estas unidades “preferidas” se denominaron Unidades SI abreviatura de “sistema internacional de unidades”. El Sistema SI tiene siete unidades fundamentales de las cuales se derivan todas las demás. Todo el trabajo científico moderno lo utiliza Unidades SI Fundamentales Cantidad física Nombre de la unidad Abreviatura Longitud metro m Masa kilogramo kg Tiempo segundo s Corriente eléctrica amper A Temperatura kelvin K Intensidad luminosa candela cd Cantidad de sustancia mol mol Una medida se expresa como el múltiplo numérico de una unidad estándar. Los múltiplos de las unidades, que son potencias de 10, se representan mediante prefijos unidos al símbolo de la unidad. Las unidades se multiplican y se dividen como números. Toda medida tiene un grado de incertidumbre o error, la magnitud del cual dependerá del instrumento utilizado y de la habilidad del operador. Al medir debe indicarse la incertidumbre asociada a la medida. Esta información será vital para quien desee repetir la experiencia o juzgar sobre su precisión. El método para citarla se describe en términos de cifras significativas. Existen un conjunto de reglas que permiten determinar el número de cifras significativas que debe tener el resultado de un cálculo. Hay que tenerlas en cuenta siempre. Estas reglas se aplican también a números en notación científica.